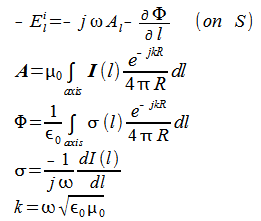2. モーメント法

2.1 モーメント法による定式化

図2-1-1のように、面状素子は格子線網に置き換え(ワイヤグリッドモデル)、 線状要素の集まりとみなすことができます。 線状導体表面S上で、電界の軸方向成分が0であるという境界条件より次式が得られます。[1]

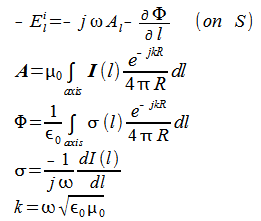(2-1-1)

ここでlは軸方向に沿った長さ、Eⁱは印加電界です。 また、時間因子e^jωtは省略します。

図2-1-1　面状・線状素子とその要素分割

各要素内では、電流(I)、電荷(σ)は一定とします。 式(2-1-1)の第1式を要素m(m=1,...N)に沿って積分すると次式が得られます。(N:線状要素の総数)

(2-1-2)

ここで要素番号は図2-1-2のように与えます。
Φ(m^-),σ(n^-)についても同様です。 また、Δl_nは要素nの長さであり、 Δl⁺_n,Δl^-_n はそれぞれ半要素ほど前後にシフトしたものです。

図2-1-2　要素番号の与え方

以上から電流I(n)についてまとめると次式が得られます。

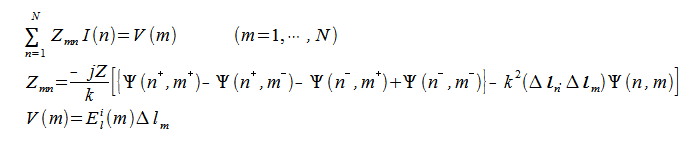(2-1-3)

ここで

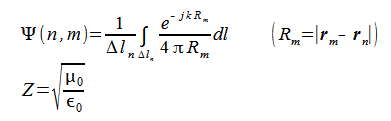(2-1-4)

なお、素子nにZ_Lの負荷がかかっている場合は対角成分を次式のように変えます。

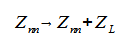(2-1-5)

行列Z_mnは複素数対称密行列です。連立一次方程式(2-1-3)を解き、 その解である電流分布I(n)(n=1,...,N)からアンテナ等の電磁気的特性を計算することができます。